Descobrindo as Tendências do Ibovespa Utilizando o Expoente de Hurst
O Expoente de Hurst é um indicador que nos permite identificar tendências em uma série temporal.
Uma tarefa hercúlea, para não dizer impossível, é tentar prever o comportamento do mercado financeiro. Sabemos que quanto menor o timeframe de análise, mais próximo de um passeio aleatório será o comportamento do ativo.
No entanto, é possível medir quão aleatório. Uma das formas de fazer isso é através do cálculo do Expoente de Hurst.
O Expoente de Hurst é um número entre 0 e 1 que mede a persistência de um processo estocástico. Um processo estocástico é dito persistente se ele tem uma tendência a se mover na mesma direção do seu passado recente. Por outro lado, um processo estocástico é dito anti-persistente se ele tem uma tendência a se mover na direção oposta do seu passado recente. Por fim, um processo estocástico é dito aleatório se ele não tem tendência a se mover em nenhuma direção.
Mas qual a vantagem de determinar se um processo estocástico é persistente, anti-persistente ou aleatório? Ora, entendendo o comportamento de um ativo, é possível determinar qual a melhor estratégia de investimento.
Por exemplo, se identificamos uma persistência, então uma estratégia de momentum (comprar ativos que estão subindo e vender ativos que estão caindo) seria mais adequada, enquanto que em um ativo anti-persistente, estratégias de reversão à média (comprar ativos que estão caindo e vender ativos que estão subindo) se tornam mais atrativas.
➡️ Veja: Screening do Expoente de Hurst
Calculando o Expoente de Hurst
De forma simplificada, o Expoente de Hurst é derivado da autocorrelação de uma série temporal. Para calculá-lo, precisamos computar a autocorrelação de um processo estocástico para diferentes lags, ou seja, a relação daquela série com ela mesma em diferentes momentos no tempo.
Existem duas formas principais de se calcular o Expoente de Hurst: utilizando o Rescaled Range ou o Detrended Fluctuation Analysis (DFA). Neste post, utilizaremos o método DFA, uma vez que ele não pressupõe que a série temporal seja estacionária.
Detrended Fluctuation Analysis (DFA)
A ideia por trás do DFA é a seguinte: primeiro definimos um range de lags \(\tau\) que queremos analisar (por exemplo, entre 2 e 200). Em seguida, calculamos a diferença entre o valor da série temporal no momento \(t\) e o valor da série temporal no momento \(t + \tau\) para cada \(\tau\) no range definido anteriormente. Por fim calculamos o desvio-padrão \(\sigma_\tau\) dessas diferenças.
Uma vez que temos o desvio-padrão \(\sigma_\tau\) para cada \(\tau\), podemos calcular o Expoente de Hurst \(H\) através da seguinte relação:
\[\sigma_\tau \propto \tau^H\]
Ou seja, se plotarmos \(\log(\sigma_\tau)\) em função de \(\log(\tau)\), o Expoente de Hurst \(H\) será o coeficiente angular da reta que melhor se ajusta aos pontos.
Embora a escolha dos lags seja de certa forma arbitrária, mais para frente vamos analisar o impacto dessa escolha no cálculo do Expoente de Hurst.
Interpretando o Expoente de Hurst
Vimos que \(H\) é um número entre 0 e 1 que mede a persistência de um processo estocástico. Mas como interpretar esse número?
Embora a análise matemática esteja fora do escopo desse post, podemos dizer que:
- Se \(H = 0.5\), então a série é dita aleatória.
- Se \(H > 0.5\), então a série é dita persistente (em tendência).
- Se \(H < 0.5\), então a série é dita anti-persistente (em reversão).
Quanto mais próximo de \(1\) ou \(0\), mais forte é a tendência ou reversão, respectivamente. Do mesmo modo, quanto mais nas "redondezas" de \(0.5\), mais próximo de um passeio aleatório é o comportamento do ativo.
Calculando o Expoente de Hurst com Python
Todo cálculo descrito acima pode ser sumarizado na seguinte função em Python:
import numpy as np
def hurst(price, min_lag=2, max_lag=100):
lags = np.arange(min_lag, max_lag + 1)
sigmas = [np.std(np.subtract(price[tau:], price[:-tau])) for tau in lags]
H, c = np.polyfit(np.log10(lags), np.log10(sigmas), 1)
return H, c, lags, sigmasRepare que a função acima recebe como parâmetros a série de preços price e o intervalo para o cálculo dos lags representado como min_lag e max_lag.
A função np.polyfit calcula a regressão linear dos logs de lags e sigmas e retorna a tupla (H, c) onde H é o Expoente de Hurst e c é o coeficiente linear da reta.
Atenção: uma vez que estamos utilizando o método DFA, não precisamos nos preocupar com a estacionariedade da série temporal. Em outras palavras, podemos utilizar diretamente a série de preços. Outros métodos como o Rescaled Range pressupõe uma estacionariedade, de modo que nesses casos utiliza-se tanto uma série de retornos ou a log diferença dos preços.
Analisando o Expoente de Hurst do Ibovespa
Agora que já entendemos o conceito do Expoente de Hurst e temos uma função para cálculá-lo, chegou a hora de vermos sua aplicabilidade na prática.
Para esse estudo vamos utilizar dados do Ibovespa de 1995 até 2022. A ideia responder a pergunta: no longo prazo, existem padrões de comportamento consistentes na bolsa brasileira?
Começaremos carregando os dados necessários:
import pandas as pd
df = pd.read_csv('../data/IBOV_1995_2022.csv', index_col=0, header=0)
df
| Close | |
|---|---|
| Date | |
| 1995-01-02 | 4301.00 |
| 1995-01-03 | 4098.00 |
| 1995-01-04 | 3967.90 |
| 1995-01-05 | 4036.70 |
| 1995-01-06 | 3827.40 |
| ... | ... |
| 2022-12-23 | 109697.57 |
| 2022-12-26 | 108737.75 |
| 2022-12-27 | 108578.20 |
| 2022-12-28 | 110236.71 |
| 2022-12-29 | 109734.60 |
6931 rows × 1 columns
Certo! Já temos nosso dataframe carregado. Vamos então testar a função hurst definida anteriormente:
series = df["Close"].values
H, c, lags, sigmas = hurst(series, 2, 200)
print(f"Hurst IBOV:\t{H:.4f}")Hurst IBOV: 0.4426
Vamos entender o que foi feito. Em primeiro lugar transformamos o dataframe em uma série de preços, compatível com a função definida. Fazemos isso através da propriedade .values.
Depois, chamamos a função hurst utilizando o range de 2 a 200. Isso significa que, no cálculo do DFA, o \(\tau\) assumirá todos os valores dentro desse intervalo.
Por fim, a variável H é o valor do Expoente de Hurst dessa série. Como vimos acima, o valor de \(0.4426\) classifica o Ibovespa, nesse período e para esses lags, como uma série essencialmente de reversão à média.
Verificando a Regressão Linear
Lembre-se que \(H\) é o coeficiente angular da regressão linear do gráfico \(\log(\tau)\) vs \(\log(\sigma_\tau)\). Vamos verificar se, de fato, a regressão é visível:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(2, 1, figsize=(8, 10))
df["Close"].plot(ax=ax[0], rot=45, xlabel="")
ax[0].set_title("IBOV")
ax[1].plot(np.log10(lags), H * np.log10(lags) + c, color="red")
ax[1].scatter(np.log10(lags), np.log10(sigmas))
ax[1].set_title(f"IBOV (H = {H:.4f})")
ax[1].set_xlabel(r"log($\tau$)")
ax[1].set_ylabel(r"log($\sigma_\tau$)")
plt.subplots_adjust(hspace=0.4)
plt.show()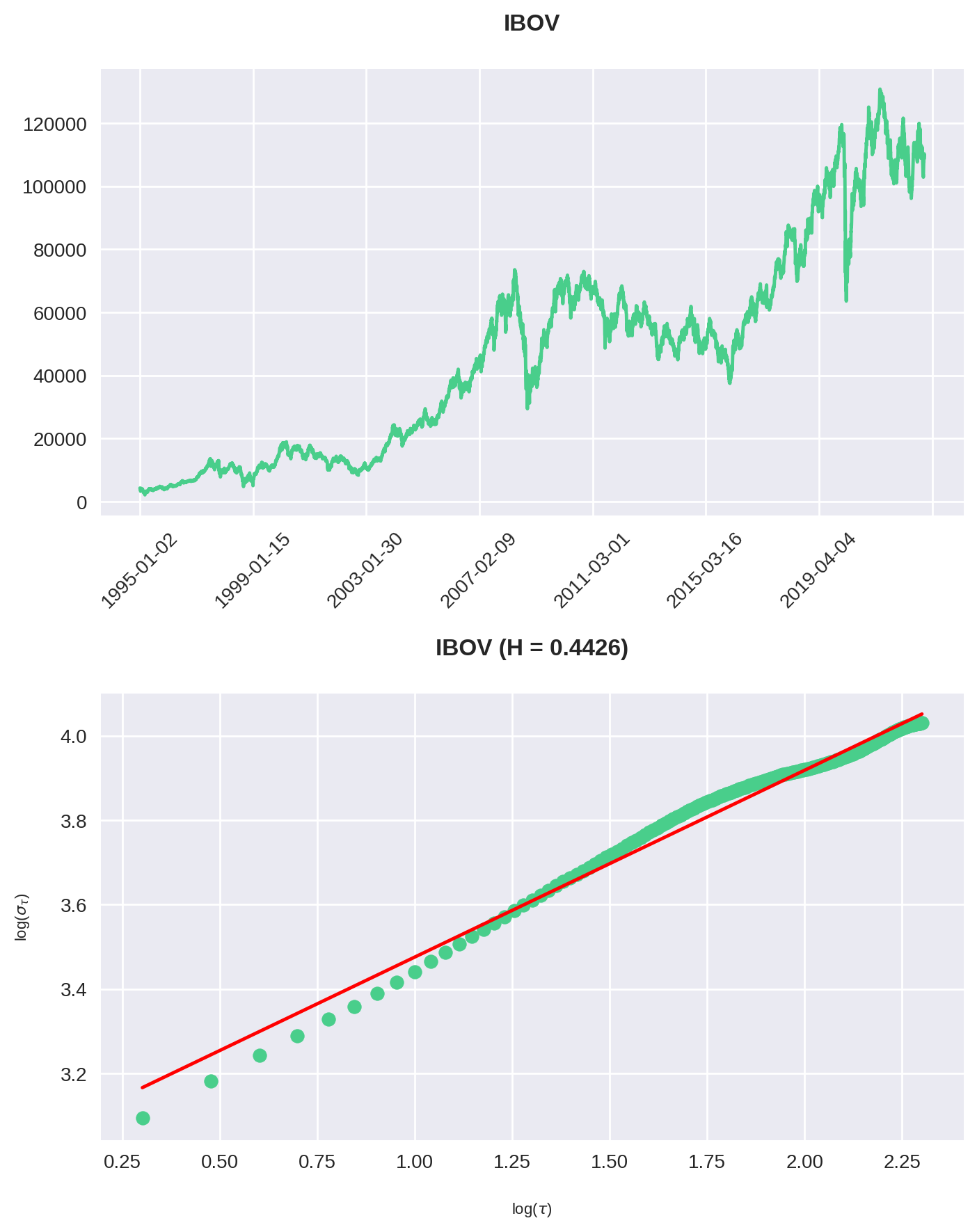
No gráfico superior plotamos o valor do Ibovespa no período. Abaixo, temos o scatter plot das nossas séries logarítimicas, enquanto a linha vermelha é a reta que melhor se adequa a esses pontos. Visualmente vemos que, de fato, a regressão é coerente, e o coeficiente angular \(H = 0.4426\) decreta então que a série é de reversão à média.
A Influência do Lag
Quando calculamos \(H\), definimos de forma arbirária um max_lag = 200. Será que a classificação da série mudaria para diferentes valores de max_lag?
print(f"Hurst (Max Lag = 20):\t{hurst(series, 2, 20)[0]:.4f}")
print(f"Hurst (Max Lag = 50):\t{hurst(series, 2, 50)[0]:.4f}")
print(f"Hurst (Max Lag = 100):\t{hurst(series, 2, 100)[0]:.4f}")
print(f"Hurst (Max Lag = 500):\t{hurst(series, 2, 500)[0]:.4f}")Hurst (Max Lag = 20): 0.5195
Hurst (Max Lag = 50): 0.5315
Hurst (Max Lag = 100): 0.4967
Hurst (Max Lag = 500): 0.3668
Aqui chegamos ao nosso primeiro problema. De fato, parece que o cálculo do Expoente de Hurst é sensível à escolha dos lags. Vemos que para max_lag = 20 e max_lag = 50 a série é persistente, praticamente aleatória para max_lag = 100, e fortemente anti-persistente quando max_lag = 500. Como podemos intepretar esse fenômeno?
Recordemos que o Hurst é oriundo da autocorrelação da série. Ora, quando mudamos o lag, mudamos a janela onde estamos olhando essa autocorrelação. É perfeitamente possível que em uma janela menor, por exemplo quando max_lag = 20, observemos uma certa propriedade, mas quando olhamos uma janela maior (por exemplo max_lag = 200), observamos outra propriedade.
Isso é intuitivo quando pensamos nos gráficos dos ativos. Não é comum termos um determinado ativo em uma tendência de curto prazo totalmente diferente da de longo prazo? Na prática, a nossa escolha do max_lag nos diz sob qual lente queremos análisar a memória da série.
Vamos observar o comportamento do Hurst quando variamos max_lag:
max_lags = np.arange(10, 1000 + 1)
all_hursts = [hurst(series, 2, max_lag)[0] for max_lag in max_lags]
plt.figure(figsize=(12,6))
plt.plot(max_lags, all_hursts, marker='o')
plt.axhline(y=0.52, color='pink', linestyle='--')
plt.axhline(y=0.50, color='r', linestyle='--')
plt.axhline(y=0.48, color='pink', linestyle='--')
plt.xlabel('Max Lags')
plt.ylabel('Hurst Values')
plt.title('Hurst Values vs Max Lags')
plt.show()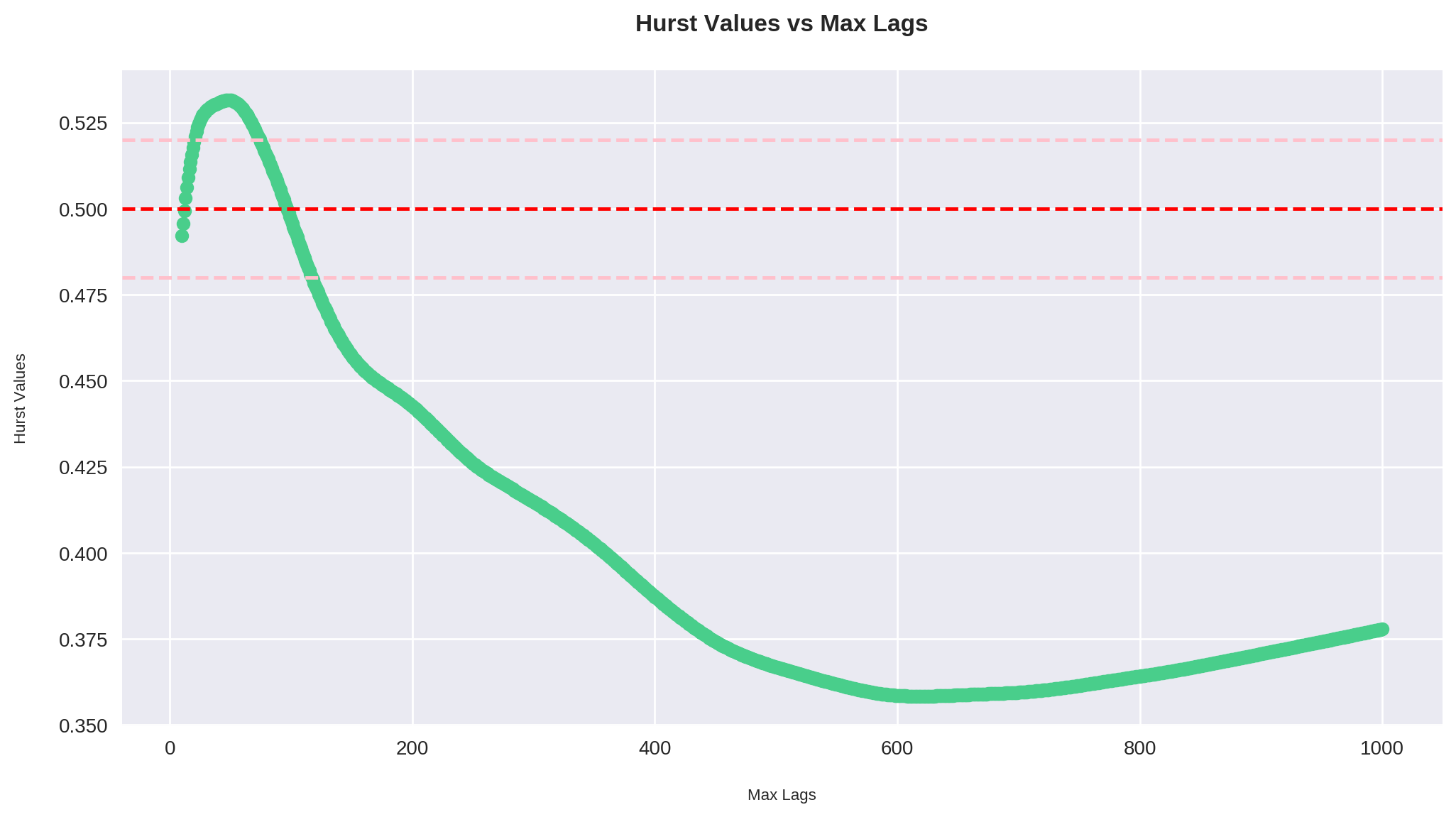
Aqui plotamos todos os valores de \(H\) quando max_lag varia entre 10 e 1000.
Sem surpresas, observamos que valores menores do lag vivem mais perto da "zona de aleatoriedade" (digamos entre 0.48 e 0.52). O máximo da tendência ocorre por volta de max_lag = 50, e a partir daí o Expoente de Hurst cai vertiginosamente passando por 0.5 mais ou menos em max_lag = 100, e buscando seu mínimo por volta de max_lag = 600.
Intepretando o Comportamento do Expoente de Hurst
O gráfico acima nos deixa algumas lições. Primeiro, que no curtíssimo prazo a série se aproxima de um passeio aleatório, ou seja, é inútil buscar algum comportamento persistente ou anti-persistente.
No entanto, vemos que por volta dos 50 períodos (digamos entre 2 e 3 meses), é sim possível identificar uma persistência no Ibovespa. Em outras palavras, existem tendências de 2 a 3 meses que podem ser aproveitadas.
Por fim, fica bastante claro que no longo prazo o Ibovespa apresenta um comportamento anti-persistente, ou seja, de reversão à média, especialmente se olhamos janelas acima de 200 períodos (digamos a partir de 1 ano.)
A Influência do Tamanho da Série
Vimos que a escolha do lag impacta drasticamente a classificação da série. Mas e o tamanho do dataset em si? Aqui calculamos a propriedade ao longo de 28 anos. Mas e se olhássemos em intervalos menores, por exemplo de 4 em 4 anos?
Pelas mesmas razões expostas acimas, também devemos esperar variações. Afinal, já vimos que mesmo que em um longo período a série seja anti-persistente, é perfeitamente possível que ela tenha janelas de persistência. Assim, se em 28 anos temos a predominância de uma característica, pode ser que em 4 anos específicos seja outra característica que impere.
Vamos verificar se há alguma característica que se mantenha constante quando dividimos nosso dataset. Para isso, irei dividir os 28 anos em 7 períodos de 4 anos, representando os mandatos presidenciais, normalmente associados a mudanças macroeconômicas.
Comecemos criando uma forma de agrupar nosso dataframe por ano:
df.index = pd.to_datetime(df.index)
# Create a year column for grouping
df['Year'] = df.index.year
# Create a period column for grouping every 4 years
df['Period'] = (df['Year'] - 1995) // 4
# Group the DataFrame into chunks of 4 years
groups = df.groupby('Period')
df
| Close | Year | Period | |
|---|---|---|---|
| Date | |||
| 1995-01-02 | 4301.00 | 1995 | 0 |
| 1995-01-03 | 4098.00 | 1995 | 0 |
| 1995-01-04 | 3967.90 | 1995 | 0 |
| 1995-01-05 | 4036.70 | 1995 | 0 |
| 1995-01-06 | 3827.40 | 1995 | 0 |
| ... | ... | ... | ... |
| 2022-12-23 | 109697.57 | 2022 | 6 |
| 2022-12-26 | 108737.75 | 2022 | 6 |
| 2022-12-27 | 108578.20 | 2022 | 6 |
| 2022-12-28 | 110236.71 | 2022 | 6 |
| 2022-12-29 | 109734.60 | 2022 | 6 |
6931 rows × 3 columns
Agora que cada linha foi classificada como um período indo de 0 a 6 (pertencente a cada uma das janelas de 4 anos a partir de 1995), podemos ir adiante e calcular o Expoente de Hurst utilizando max_lag = 200.
for name, period_df in groups:
max_year = period_df['Year'].max()
min_year = period_df['Year'].min()
series = period_df["Close"].values
H, c, lags, sigmas = hurst(series, 2, 200)
fig, ax = plt.subplots(3, 1, figsize=(8, 16))
# First plot the price series during the period
period_df["Close"].plot(ax=ax[0], rot=45, xlabel="")
ax[0].set_title(f"IBOV ({min_year}-{max_year})")
# Then plot the linear regression
ax[1].plot(np.log10(lags), H * np.log10(lags) + c, color="red")
ax[1].scatter(np.log10(lags), np.log10(sigmas))
ax[1].set_title(f"H = {H:.4f} ({min_year}-{max_year})")
ax[1].set_xlabel(r"log($\tau$)")
ax[1].set_ylabel(r"log($\sigma_\tau$)")
# Finally plot the Hurst values for different max lags
max_lags = np.arange(10, 250 + 1)
all_hursts = [hurst(series, 2, max_lag)[0] for max_lag in max_lags]
ax[2].plot(max_lags, all_hursts, marker='o')
ax[2].axhline(y=0.52, color='pink', linestyle='--')
ax[2].axhline(y=0.50, color='r', linestyle='--')
ax[2].axhline(y=0.48, color='pink', linestyle='--')
ax[2].set_xlabel('Max Lags')
ax[2].set_ylabel('Hurst Values')
ax[2].set_title(f'Hurst Values vs Max Lags ({min_year}-{max_year})')
plt.subplots_adjust(hspace=0.6)
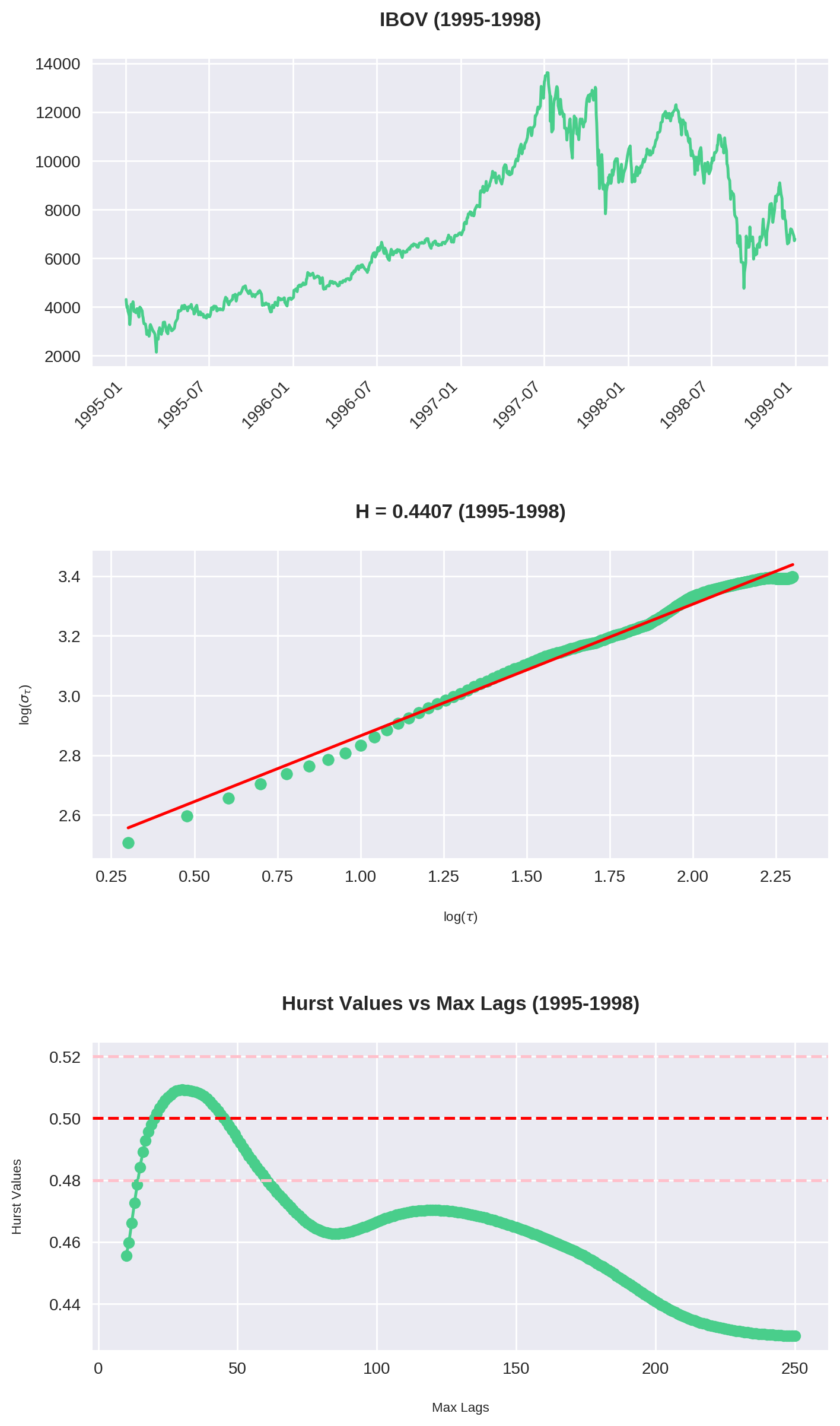

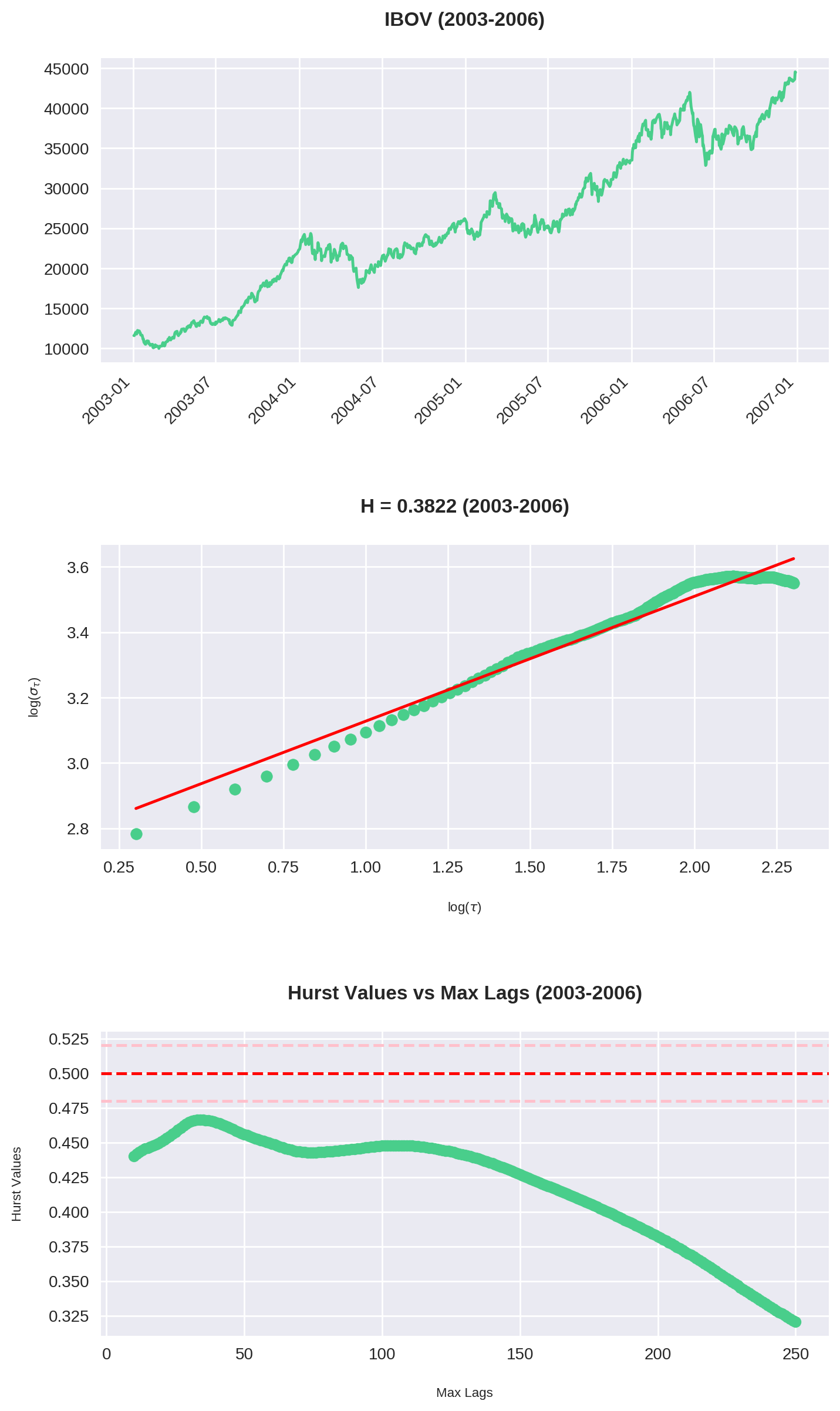
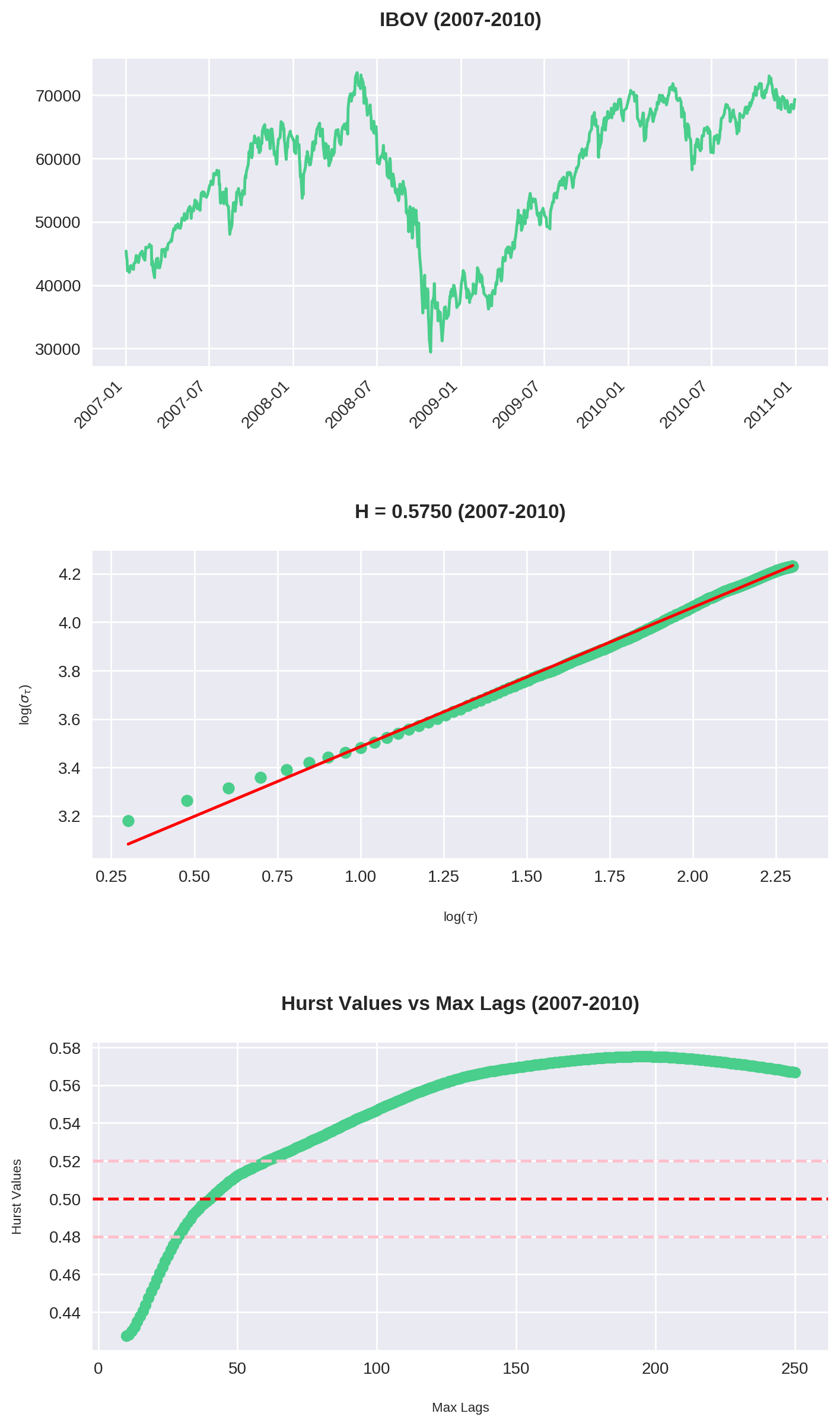
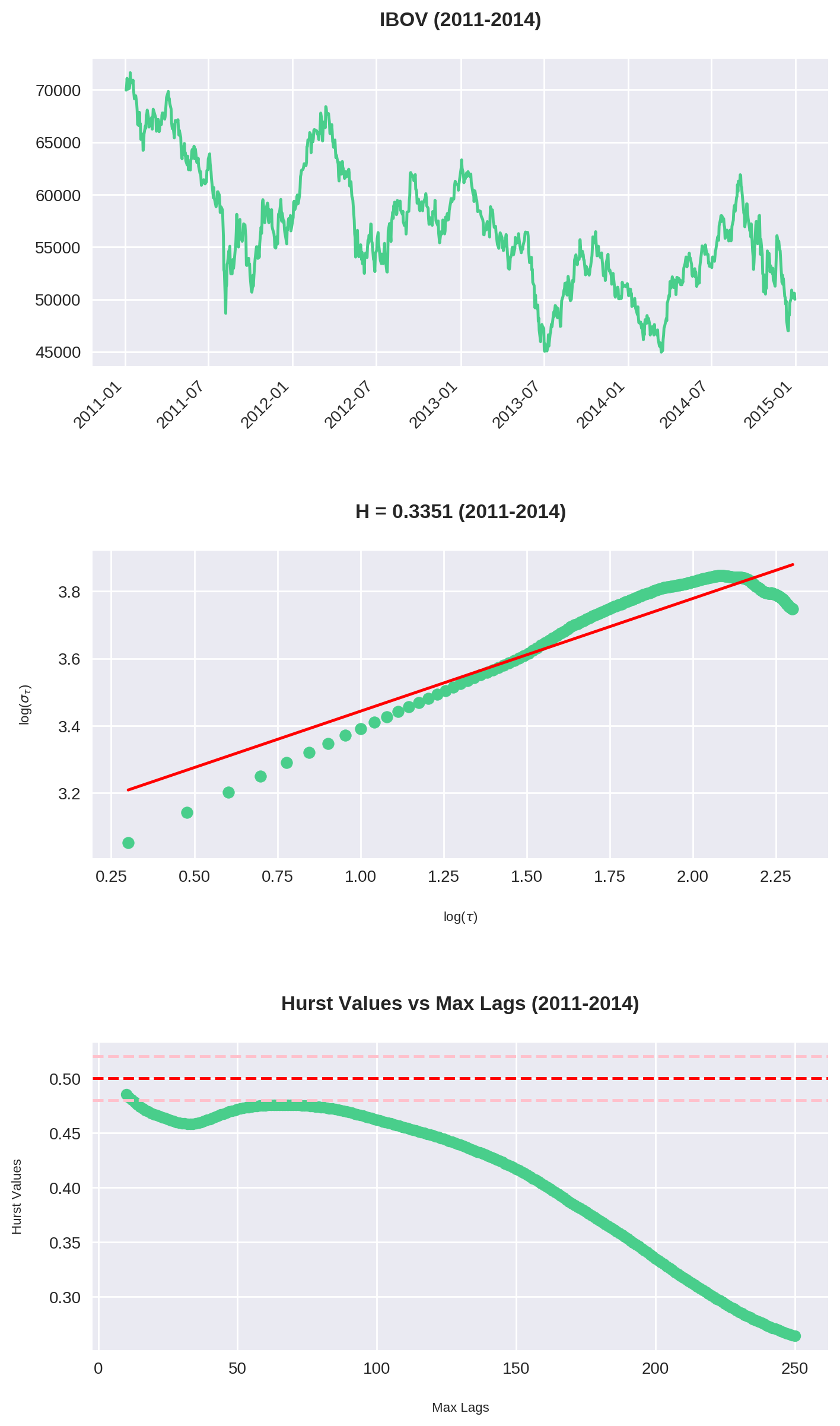
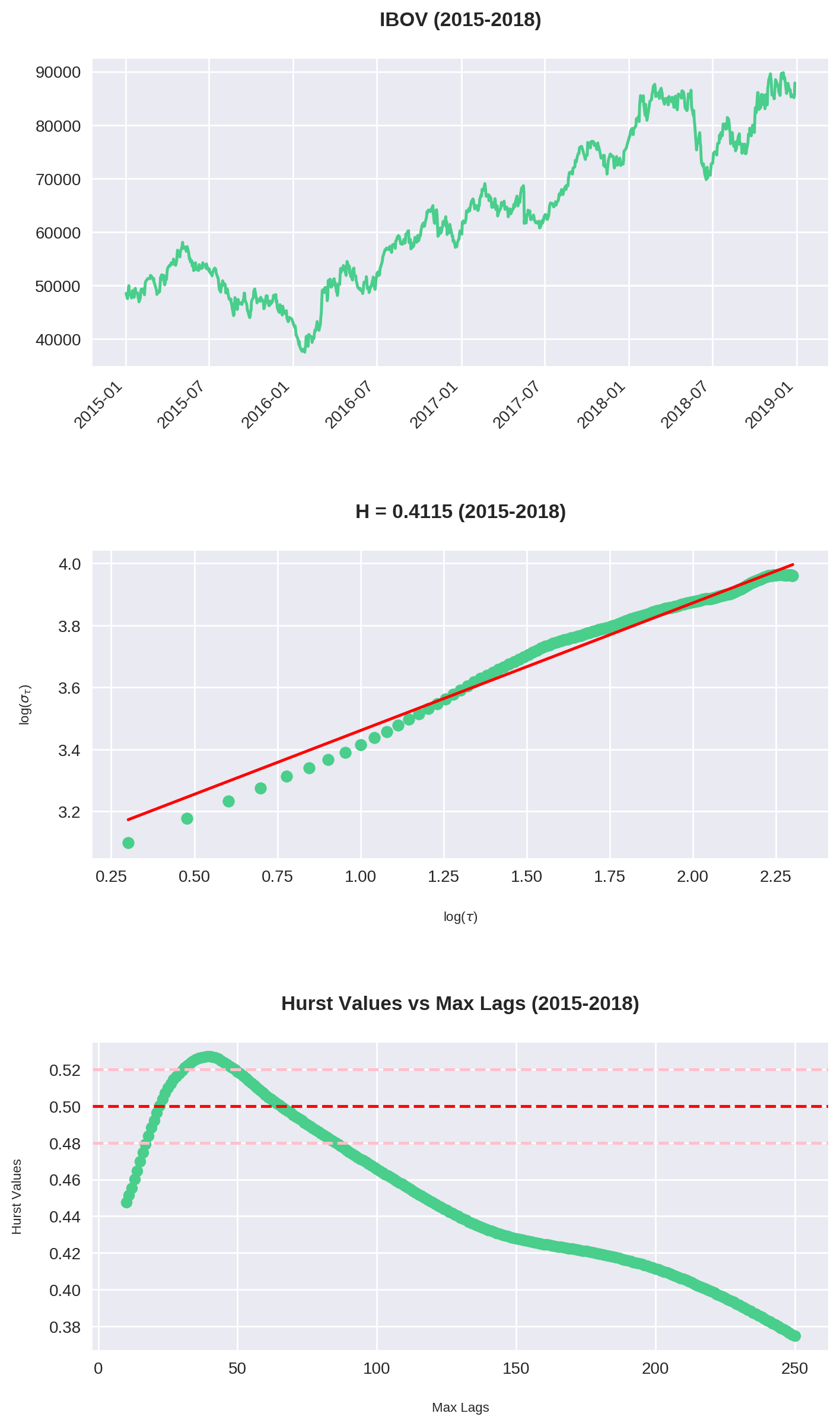
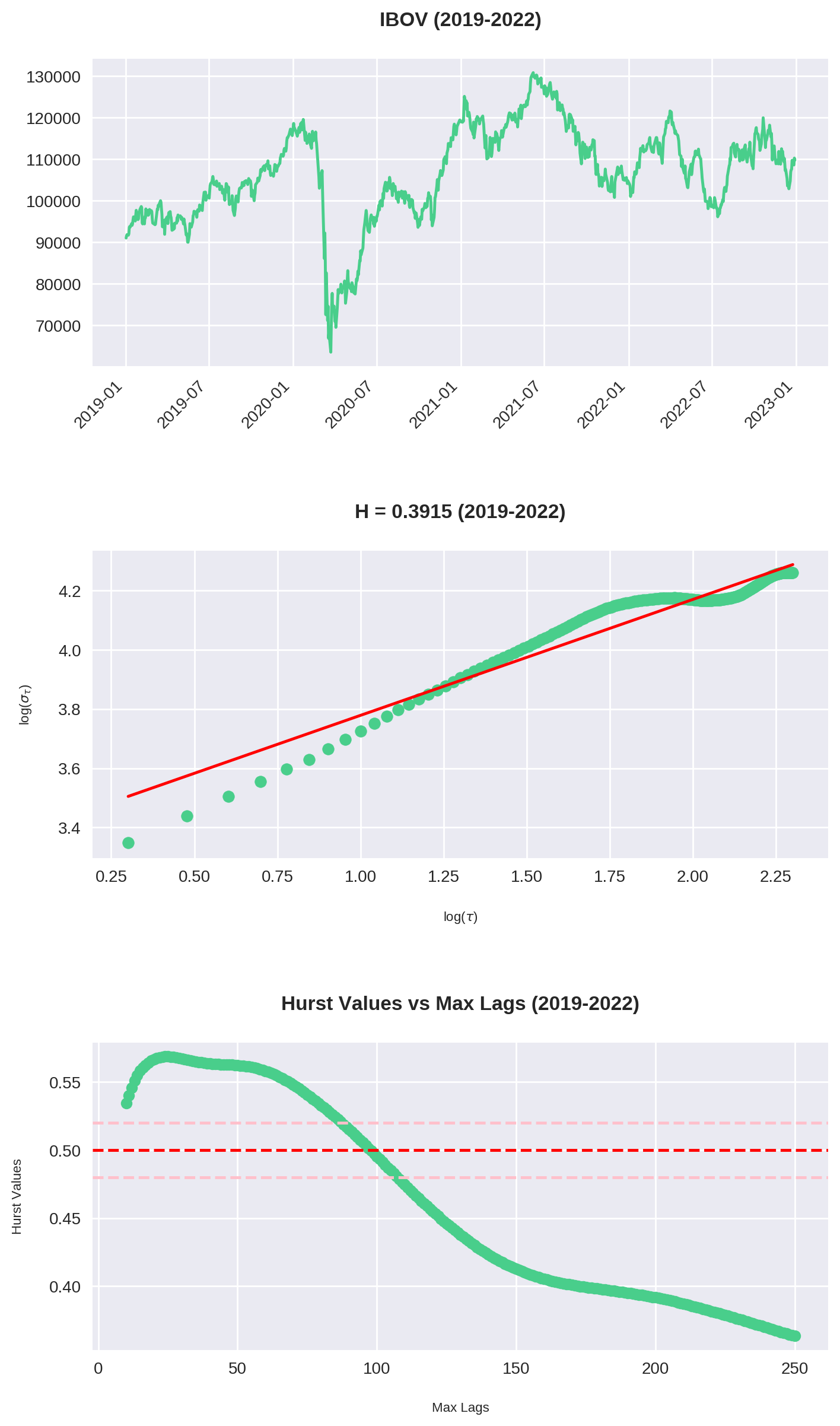
O código acima é uma junção do que fizemos até agora. Repare que plotamos 3 gráficos:
- O gráfico do Ibovespa no período
- O Expoente de Hurst para
max_lag = 200 - O comportamento de \(H\) para cada valor de
max_lagsde 10 até 250.
Podemos tirar várias interpretações interessantes desses gráficos.
Nossos olhos pregam peças
Em diversas situações o gráfico parece claramente em tendência. No entanto, a análise de Hurst o classifica como reversão à média. Observe em especial o período entre 2003-2006: a bolsa mais que triplicou, mas \(H = 0.3822\), indicando uma forte anti-persistência. Por quê? Não se esqueça que estamos olhando uma janela de 200 períodos dentro de um intervalo de 1000 data points. Ou seja, por mais que haja momentos de forte alta, ainda assim pode-se observar longos períodos de reversão.
Similarmente, entre 2007-2010 o gráfico parece estar de lado, embora na realidade foi o momento de maior tendência.
O Ibovespa reverte à média
Dos 7 intervalos calculados, em 6 (!!) podemos classificar a série como anti-persistente. Isso é condizente com nossa análise no dataset inteiro. Veja que aqui utilizamos max_lag = 200, ou seja, observamos que mesmo em diversos recortes o Ibovespa reverteu à média dentro do período de 1 ano.
Importante: "reversão à média" não significa necessariamente que o ativo volta ao preço anterior, mas sim que, entrando nessa "fase", dentro do período estudado, quedas tem maior probabilidade de serem acompanhadas por altas, e vice-versa.
As maiores tendências ocorrem entre 2-3 meses
Analisando o gráfico de Hurst x Max Lag, vemos que a história se repete: há uma máxima entre 40-60 períodos (em dias corridos, por volta de 2 e 3 meses). Consistentemente esse é o ponto onde o Ibovespa assume sua tendência mais forte (com exceção de 2007-2010).
Isso confirma nossa tese original: embora o Ibovespa tenha um forte componente de reversão em janelas maiores, há períodos de 2 a 3 meses de duração onde observa-se uma maior tendência (ou no mínimo, um enfraquecimento da reversão).
Como Operar o Expoente de Hurst?
Bem, todo esse papo é bastante interessante e saber se o Ibovespa está em tendência é legal mas, na prática, como podemos utilizar o Hurst nas tomadas de decisão?
Hurst como critério de escolha de estratégias
A forma mais intuitiva é utilizá-lo como critério para se escolher o tipo de estratégia a ser aplicada. Por exemplo, no nosso Guia de Estratégias classificamos diversas estratégias quantitativas como tendência ou volatilidade.
Utilizando o Expoente de Hurst você pode determinar em qual regime o ativo se encontra, e daí buscar a estratégia mais adequada. Isso faz com que você evite aplicar uma estratégia de tendência em um ativo em reversão, por exemplo. Confira o Guia de Estratégias para saber qual estratégia melhor se encaixa no ativo que você quer operar!
Hurst como filtro de momentum
Outra vantagem do Expoente de Hurst é utilizá-lo como um filtro de momentum. Ora, em uma estratégia de Factor Investing esse cálculo pode ser feito para montar um portfólio que se encaixe nesse perfil. Nosso screening de Momentum também pode ser utilizado para fortalecer a análise.
É possível montar uma estratégia onde compra-se (ou vende-se) os ativos em maior tendência, fazendo um rebalanceamento periódico. Note, no entanto, que o horizonte do trade deve ser compatível com o valor de max_lags escolhido.
Hurst como validação de estratégias
É comum que uma estratégia quantitativa passe por momentos onde ela não performa. Ora, se a sua estratégia é de tendência e o ativo entrou em um regime de mean reversal, é esperado que os resultados não sejam tão bons. Portanto, na hora de avaliar a eficácia de uma estratégia, é interessante utilizar o \(H\) para entender em que momento do mercado aquele trade foi executado.
Limitações
Fica claro desde o início que o Expoente de Hurst é sensível a duas variáveis:
- O tamanho do dataset
- O valor de
max_lag
Portanto, toda análise deve levar esses dois parâmetros em consideração. Utilizar o Hurst em timeframes conflitantes pode fazer você perder dinheiro.
Por fim, o Expoente de Hurst por si só não tem nenhum valor preditivo. É claro que, da mesma forma como no cálculo de momentum, espera-se que um ativo que esteja em tendência, tudo mais constante, continue em tendência (1ª Lei de Newton). É razoável assumir que a propriedade vá se manter, mas apenas uma análise detalhada em diversos recortes como fizemos aqui pode dar mais robustez ao cálculo.
O Expoente de Hurst não determina a direção da tendência
Embora utilizemos Hurst para descobrir se um ativo está em tendência, ele não faz juízo sobre sua direção. Ou seja, um ativo em tendência pode significar tanto tendência de alta quanto de baixa.
Para determinar a direção podem ser utilizadas outras técnicas:
- Verifica-se se o ativo está no Éden dos Traders;
- Verifica-se a variação do preço do ativo em uma janela compatível. Para isso, pode-se utilizar o ranking de ativos do QuantBrasil;
- Direção de alguma média móvel (ex: a direção onde a MM50 está apontada).
Screening do Expoente de Hurst
No QuantBrasil é possível visualizar qual o valor de \(H\) para os ativos mais líquidos do Ibovespa.
Esse screening é atualizado diariamente e leva em consideração os preços dos ativos no último ano, e um max_lag de 50 períodos.
Esses valores foram escolhidos pois favorecem trades de curto e médio prazo. Assim, traders podem utilizar o Guia de Estratégias para buscar uma estratégia compatível com a classificação do ativo nesse período.
De forma resumida, o screening do Expoente de Hurst diz se, ao longo do último ano, analisando-se janelas de 50 dias, há alguma propriedade que possa ser explorada (persistência ou anti-persistência).
Se você gostaria de ter acesso a uma ferramenta capaz de calcular a mesma análise que fizemos para o Ibovespa, mas para os seus ativos favoritos, crie sua conta no QuantBrasil e fique ligado nas novidades!
Conclusão
O Expoente de Hurst pode ser utilizado para classificar um processo estocástico (como uma série de preços) em persistente, anti-persistente e aleatório. Uma série persistente é dita em tendência, enquanto uma série anti-persistente é dita em reversão à média.
Verificamos que ao longo de 28 anos o Ibovespa apresenta consistentes intervalos de reversão à média em prazos maiores (acima de 200 períodos). Isso significa que, mesmo em períodos de forte alta como entre 2003-2006, a bolsa brasileira apresenta longos momentos de reversão.
Por fim, constatamos que o Ibovespa apresenta maior probabilidade de tendência em janelas de 2 a 3 meses. Essa informação pode ser utilizada como filtro para se buscar as melhores estratégias para o momento de um ativo, além de ajudar na montagem da carteira.
Se você tem interesse em aprofundar as análises do Expoente de Hurst, crie sua conta no QuantBrasil e aguarde as novidades. Abraços e até a próxima!
