Entenda o Drawdown e Calcule essa Medida de Volatilidade para Qualquer Ativo
Utilize Python para calcular as maiores quedas de um ativo em um determinado período de tempo.
O drawdown é uma importante medida de volatilidade para os investidores. De forma simples, o drawdown é calculado como a porcentagem de quanto um ativo, fundo ou portfólio caiu em relação ao seu topo.
Suponha que o Ibovespa esteja cotado a 100.000 pontos em uma determinada data. Durante os próximos dias, ele cai para 90.000 sem superar a marca dos 100.000 pontos. O drawdown nesse período foi de 10%.
Agora, se depois de alcançar os 90.000 pontos o Ibovespa suba para 115.000 pontos, o próximo drawdown será calculado utilizando o mais novo topo. Nesse caso, se ele cair para 100.000 logo em seguida, o drawdown será de:
\[ \dfrac{(115.000 - 100.000)}{115.000} \times 100 \approx 13\% \]
A importância do drawdown
O drawdown é bastante utilizado para medir a volatilidade, ou o risco, de um determinado investimento. Se dois ativos, A e B, possuem o mesmo retorno ao longo de um período, mas o drawdown de A é menor que o de B, o ativo A tende a ser preferível.
A discussão entre volatilidade x risco é extensa e está além do escopo desse artigo. No entanto, como exemplos, se um investimento observa quedas maiores, o investidor incorre no risco:
- de ter uma chamada de margem (caso alavancado),
- de encerrar o investimento prematuramente antes da recuperação (comum em fundos de investimento),
- e de precisar resgatar em um momento de forte queda (devido a uma emergência ou até mesmo para a aposentadoria).
No caso específico de uma estratégia de trade, um menor drawdown significa uma menor exposição ao risco, e portanto minimizá-lo pode ser interessante mesmo que a rentabilidade da estratégia caia.
O que é melhor: uma estratégia A com rentabilidade de 20% e um drawdown de 15%, ou uma estratégia B com rentabilidade de 25% e drawdown de 40%? Mesmo que a resposta correta não exista, uma vez que é dependente da gestão de risco e perfil de cada pessoa, calcular o drawdown é de suma importância para qualquer investimento.
Calculando o drawdown do Ibovespa
Nossa primeira tarefa será calcular o drawdown máximo do Ibovespa em um determinado período. É importante entender o termo drawdown máximo: ele é a medida do maior drawdown ocorrido no período estabelecido. No exemplo anterior, a primeira queda foi de 100.000 para 90.000 (drawdown de 10%), e depois de 115.000 para 100.000 (drawdown de 13%). Um investidor analisando esse período específico observaria que o drawdown máximo foi de 13%.
O primeiro passo é importar as bibliotecas que vamos utilizar e baixar os preços de fechamento do Ibovespa em 2020 utilizando o Yahoo Finance. Note que o ticker do Ibovespa no yfinance é ^BVSP. Os símbolos podem ser pesquisados diretamente na plataforma.
# %%capture means we suppress the output
%%capture
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
!pip install yfinance
import yfinance as yfdata = yf.download("^BVSP", start="2020-01-01", end="2020-12-31").copy()[['Adj Close']]
data.head() # returns the first 5 rows of the dataframe| Adj Close | |
|---|---|
| Date | |
| 2020-01-02 | 118573.0 |
| 2020-01-03 | 117707.0 |
| 2020-01-06 | 116878.0 |
| 2020-01-07 | 116662.0 |
| 2020-01-08 | 116247.0 |
Em seguida vamos utilizar a função cummax para criar uma nova coluna com o valor máximo de Adj Close até o elemento em questão. Repare a diferença entre cummax e max: enquanto cummax retorna, para cada elemento, o valor máximo anterior ou igual a ele, max retorna o valor máximo na coluna inteira, independente de ter ocorrido antes ou depois do elemento.
data["Max"] = data['Adj Close'].cummax()
data.head(20)| Adj Close | Max | |
|---|---|---|
| Date | ||
| 2020-01-02 | 118573.0 | 118573.0 |
| 2020-01-03 | 117707.0 | 118573.0 |
| 2020-01-06 | 116878.0 | 118573.0 |
| 2020-01-07 | 116662.0 | 118573.0 |
| 2020-01-08 | 116247.0 | 118573.0 |
| 2020-01-09 | 115947.0 | 118573.0 |
| 2020-01-10 | 115503.0 | 118573.0 |
| 2020-01-13 | 117325.0 | 118573.0 |
| 2020-01-14 | 117632.0 | 118573.0 |
| 2020-01-15 | 116414.0 | 118573.0 |
| 2020-01-16 | 116704.0 | 118573.0 |
| 2020-01-17 | 118478.0 | 118573.0 |
| 2020-01-20 | 118862.0 | 118862.0 |
| 2020-01-21 | 117026.0 | 118862.0 |
| 2020-01-22 | 118391.0 | 118862.0 |
| 2020-01-23 | 119528.0 | 119528.0 |
| 2020-01-24 | 118376.0 | 119528.0 |
| 2020-01-27 | 114482.0 | 119528.0 |
| 2020-01-28 | 116479.0 | 119528.0 |
| 2020-01-29 | 115385.0 | 119528.0 |
Agora que temos o valor do último topo (Max) para cada linha, podemos calcular o drawdown (em %):
data["Delta"] = data["Max"] - data["Adj Close"]
data["Drawdown"] = 100 * (data["Delta"] / data["Max"])
data.head(20)| Adj Close | Max | Delta | Drawdown | |
|---|---|---|---|---|
| Date | ||||
| 2020-01-02 | 118573.0 | 118573.0 | 0.0 | 0.000000 |
| 2020-01-03 | 117707.0 | 118573.0 | 866.0 | 0.730352 |
| 2020-01-06 | 116878.0 | 118573.0 | 1695.0 | 1.429499 |
| 2020-01-07 | 116662.0 | 118573.0 | 1911.0 | 1.611665 |
| 2020-01-08 | 116247.0 | 118573.0 | 2326.0 | 1.961661 |
| 2020-01-09 | 115947.0 | 118573.0 | 2626.0 | 2.214669 |
| 2020-01-10 | 115503.0 | 118573.0 | 3070.0 | 2.589122 |
| 2020-01-13 | 117325.0 | 118573.0 | 1248.0 | 1.052516 |
| 2020-01-14 | 117632.0 | 118573.0 | 941.0 | 0.793604 |
| 2020-01-15 | 116414.0 | 118573.0 | 2159.0 | 1.820819 |
| 2020-01-16 | 116704.0 | 118573.0 | 1869.0 | 1.576244 |
| 2020-01-17 | 118478.0 | 118573.0 | 95.0 | 0.080119 |
| 2020-01-20 | 118862.0 | 118862.0 | 0.0 | 0.000000 |
| 2020-01-21 | 117026.0 | 118862.0 | 1836.0 | 1.544648 |
| 2020-01-22 | 118391.0 | 118862.0 | 471.0 | 0.396258 |
| 2020-01-23 | 119528.0 | 119528.0 | 0.0 | 0.000000 |
| 2020-01-24 | 118376.0 | 119528.0 | 1152.0 | 0.963791 |
| 2020-01-27 | 114482.0 | 119528.0 | 5046.0 | 4.221605 |
| 2020-01-28 | 116479.0 | 119528.0 | 3049.0 | 2.550867 |
| 2020-01-29 | 115385.0 | 119528.0 | 4143.0 | 3.466133 |
Pronto! O código acima nos diz qual o drawdown atual do ativo, dentro do período selecionado, em qualquer momento do tempo. Assim, podemos rapidamente dizer que o drawdown do Ibovespa em 2020, no dia 27 de Janeiro de 2020, era de 4,22%.
Como fazemos então para calcular o drawdown máximo no período?
max_drawdown = data["Drawdown"].max()
max_drawdown
46.815808848136
Simples assim. O drawdown máximo do Ibovespa em 2020 foi de impressionantes 46,18% (2020 não foi pra amadores!)
Encontrando o período de máximo drawdown no gráfico
Como sempre, faz parte das nossas análises facilitar o entendimento com a melhor visualização possível. Vamos então identificar, via código, os pontos que compreenderam o drawdown máximo de 2020 e marcá-los em um gráfico.
# Get the position of the point with maximum Drawdown value
bottom_day = np.argmax(data['Drawdown'])
bottom_index = data[['Drawdown']].index.get_loc(bottom_day)
print(bottom_day, bottom_index, sep="\n")2020-03-23 00:00:00 54
Repare que nós utilizamos argmax para retornar o índice (no caso, o dia) onde observamos o maior drawdown. Esse dia é o fundo do mercado e foi observado na linha 55 (índice número 54).
Para identificar o topo, vamos achar o valor máximo do Ibovespa na data do fundo, e buscar quando foi a primeira ocorrência desse preço.
# Get the position of the point with peak value before bottom
max_value = data.iloc[bottom_index]['Max']
top_day = (data['Max'] == max_value).idxmax()
top_index = data[['Max']].index.get_loc(top_day)
print(top_day, top_index, sep="\n")2020-01-23 00:00:00 15
Dessa vez usamos idxmax para retornar a primeira ocorrência de quando o index foi igual ao valor máximo observado anteriormente ao fundo estabelecido. O topo foi definido no dia 23 de Janeiro de 2020, no 16º pregão do ano.
Plotando os pontos de topo e fundo
Com os pontos em mãos, podemos utilizar o matplotlib para visualizar esse período no gráfico:
data["Adj Close"].plot(
marker='o',
markerfacecolor="red",
markevery=[top_index, bottom_index],
)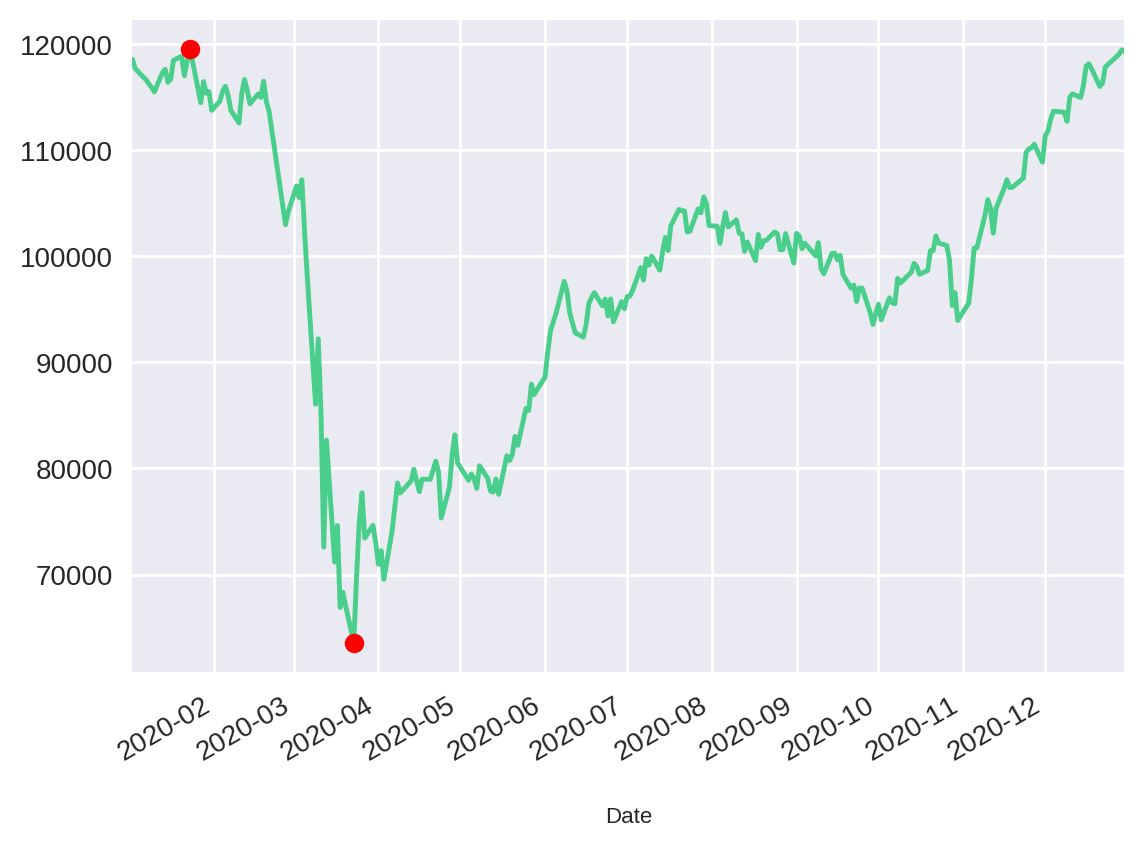
Veja como a visualização nos ajuda a confirmar que os pontos marcados em vermelho foram, de fato, os pontos que compreenderam a maior queda do Ibovespa durante o ano de 2020.
Calculando o drawdown de vários anos
Nosso código está pronto e é capaz de nos retornar o drawdown em qualquer período, para qualquer ativo. Vamos facilitar ainda mais a nossa vida e escrever um código que nos permita analisar o drawdown máximo por ano em um determinado período.
O primeiro passo é transformar o cálculo do drawdown máximo em uma função:
def get_drawdown(data, column = "Adj Close"):
data["Max"] = data[column].cummax()
data["Delta"] = data['Max'] - data[column]
data["Drawdown"] = 100 * (data["Delta"] / data["Max"])
max_drawdown = data["Drawdown"].max()
return max_drawdownAgora, vamos baixar as cotações do Ibovespa dos últimos 5 anos:
start_date = "2015-01-01"
end_date = "2020-12-31"
data = yf.download("^BVSP", start=start_date, end=end_date).copy()[['Adj Close']]
data| Adj Close | |
|---|---|
| Date | |
| 2015-01-02 | 48512.0 |
| 2015-01-05 | 47517.0 |
| 2015-01-06 | 48001.0 |
| 2015-01-07 | 49463.0 |
| 2015-01-08 | 49943.0 |
| ... | ... |
| 2020-12-22 | 116348.0 |
| 2020-12-23 | 117857.0 |
| 2020-12-28 | 119051.0 |
| 2020-12-29 | 119475.0 |
| 2020-12-30 | 119306.0 |
1480 rows × 1 columns
Nós podemos facilmente filtrar os dados por ano:
data_in_2019 = data[data.index.year == 2019]
data_in_2019
| Adj Close | |
|---|---|
| Date | |
| 2019-01-02 | 91012.0 |
| 2019-01-03 | 91564.0 |
| 2019-01-04 | 91841.0 |
| 2019-01-07 | 91699.0 |
| 2019-01-08 | 92032.0 |
| ... | ... |
| 2019-12-20 | 115121.0 |
| 2019-12-23 | 115863.0 |
| 2019-12-26 | 117203.0 |
| 2019-12-27 | 116534.0 |
| 2019-12-30 | 115964.0 |
247 rows × 1 columns
Para descobrir o drawdown anual do período estabelecido, precisamos realizar os seguintes passos:
- Identificar quais os anos estão compreendidos entre nossas datas inicial e final;
- Iterar sobre cada um dos anos e filtrar apenas os dados para aquele ano;
- Calcular o drawdown para o dataframe filtrado.
Vamos construir uma lista com os anos entre start_date e end_date:
from datetime import datetime
start = datetime.strptime(start_date, "%Y-%m-%d")
end = datetime.strptime(end_date, "%Y-%m-%d")
years = range(start.year, end.year + 1)
list(years)[2015, 2016, 2017, 2018, 2019, 2020]Com a lista definida, vamos iterar sobre cada ano, filtrar os dados necessários e adicionar o drawdown do ano em um dicionário:
drawdowns = {}
for year in years:
yearly_data = data[data.index.year == year].copy()
yearly_drawdown = get_drawdown(yearly_data)
drawdowns[year] = yearly_drawdown
drawdowns
{2015: 25.583959208985046, 2016: 12.035425490951097, 2017: 12.00544517175462, 2018: 20.35070105986104, 2019: 10.00160009600576, 2020: 46.815808848136}Pronto! Temos todos os drawdowns do Ibovespa nos últimos 5 anos de forma extremamente simples.
Calculando o drawdown de diversos ativos
Nós mencionamos anteriormente que o drawdown pode ser utilizado como uma medida comparativa entre duas estratégias de investimento. Sendo assim, é bastante útil colocar o drawdown em contexto.
Agora que calculamos o drawdown do Ibovespa nos últimos 5 anos, podemos repetir o raciocínio para diversos outros papeis da bolsa. No entanto, em vez de fazermos isso manualmente, vamos escrever um código que nos possibilite compará-los de forma bastante objetiva:
# Arbitrary list of stocks
tickers = [
"^BVSP",
"PETR4.SA",
"VALE3.SA",
"VVAR3.SA",
"EQTL3.SA",
"LREN3.SA",
"GOLL4.SA",
"BTOW3.SA",
"WEGE3.SA",
"ITUB4.SA",
"BBAS3.SA",
"B3SA3.SA",
"MOVI3.SA",
"AZUL4.SA",
"IRBR3.SA"
]
stocks = yf.download(tickers, start=start_date, end=end_date).copy()['Adj Close']
stocks| AZUL4.SA | B3SA3.SA | BBAS3.SA | BTOW3.SA | EQTL3.SA | GOLL4.SA | IRBR3.SA | ITUB4.SA | LREN3.SA | MOVI3.SA | PETR4.SA | VALE3.SA | VVAR3.SA | WEGE3.SA | ^BVSP | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | |||||||||||||||
| 2015-01-02 | NaN | 7.692603 | 16.429703 | 21.140301 | 3.882352 | 14.990000 | NaN | 13.516544 | 10.508009 | NaN | 8.683293 | 17.272886 | 6.543556 | 10.323507 | 48512.0 |
| 2015-01-05 | NaN | 7.482286 | 16.088779 | 20.464600 | 3.734117 | 14.850000 | NaN | 13.584496 | 10.215857 | NaN | 7.941135 | 17.013140 | 6.543556 | 10.393835 | 47517.0 |
| 2015-01-06 | NaN | 7.555089 | 16.313652 | 20.522499 | 3.944471 | 15.210000 | NaN | 13.804224 | 10.333539 | NaN | 7.681378 | 17.694967 | 6.543556 | 10.239674 | 48001.0 |
| 2015-01-07 | NaN | 7.854380 | 17.031767 | 20.319799 | 3.910589 | 14.550000 | NaN | 14.303653 | 10.509348 | NaN | 8.043181 | 18.344326 | 7.082436 | 10.122375 | 49463.0 |
| 2015-01-08 | NaN | 7.749222 | 17.089794 | 19.653799 | 3.882352 | 14.270000 | NaN | 14.527440 | 10.521830 | NaN | 8.562695 | 18.539129 | 7.082436 | 10.293266 | 49943.0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 2020-12-22 | 35.270000 | 59.737888 | 38.290001 | 75.970001 | 22.650000 | 23.299999 | 7.19 | 31.235180 | 43.160000 | 19.208057 | 27.280001 | 86.940002 | 15.940000 | 72.820000 | 116348.0 |
| 2020-12-23 | 37.700001 | 59.450500 | 38.919998 | 75.599998 | 22.670000 | 24.540001 | 7.24 | 31.924854 | 43.720001 | 19.823507 | 27.950001 | 87.360001 | 16.129999 | 72.620003 | 117857.0 |
| 2020-12-28 | 37.770000 | 60.946918 | 39.349998 | 77.040001 | 23.040001 | 24.250000 | 8.11 | 32.154743 | 43.970001 | 19.892996 | 28.180000 | 87.309998 | 16.590000 | 75.500000 | 119051.0 |
| 2020-12-29 | 37.669998 | 61.264038 | 39.119999 | 75.699997 | 22.980000 | 24.480000 | 8.21 | 32.084778 | 44.130001 | 20.031967 | 28.270000 | 87.070000 | 16.580000 | 75.150002 | 119475.0 |
| 2020-12-30 | 39.299999 | 61.422600 | 38.799999 | 75.610001 | 23.160000 | 24.940001 | 8.18 | 31.615000 | 43.540001 | 20.498520 | 28.340000 | 87.449997 | 16.160000 | 75.739998 | 119306.0 |
1489 rows × 15 columns
O raciocínio é o mesmo: iteraremos sobre a lista de ativos e calcularemos o drawdown anual, armazenando essa informação em um dicionário. Eis o código:
all_drawdowns = {}
for ticker in tickers:
data = stocks[[ticker]]
drawdowns = {}
for year in years:
yearly_data = data[data.index.year == year].copy()
yearly_drawdown = get_drawdown(yearly_data, column = ticker)
drawdowns[year] = yearly_drawdown
all_drawdowns[ticker] = drawdowns
all_drawdowns
{'^BVSP': {2015: 25.583959208985046, 2016: 12.035425490951097, 2017: 12.00544517175462, 2018: 20.35070105986104, 2019: 10.00160009600576, 2020: 46.815808848136}, 'PETR4.SA': {2015: 55.370760542208906, 2016: 38.864638802102405, 2017: 27.656924921683206, 2018: 46.95510222158168, 2019: 17.24379544534969, 2020: 63.35605336711879}, 'VALE3.SA': {2015: 56.08258065080083, 2016: 35.56986161485101, 2017: 28.093024393482068, 2018: 20.418006567945692, 2019: 25.93054585334471, 2020: 40.550904946181845}, 'VVAR3.SA': {2015: 82.87937752873043, 2016: 27.113703092645718, 2017: 27.897840647678603, 2018: 50.44702954161212, 2019: 36.000001430511475, 2020: 75.36057659242984}, 'EQTL3.SA': {2015: 14.331557740431938, 2016: 11.292590784644522, 2017: 11.805536665040066, 2018: 21.719273446438702, 2019: 11.631328831997262, 2020: 40.9665448071925}, 'LREN3.SA': {2015: 28.140179772014978, 2016: 21.70930481448726, 2017: 13.185765146517658, 2018: 27.71149584936101, 2019: 10.916516169469098, 2020: 50.61581662818844}, 'GOLL4.SA': {2015: 84.28665286712683, 2016: 53.83693244372522, 2017: 35.822224087185326, 2018: 61.02971679584582, 2019: 33.202998881506915, 2020: 85.65941097556318}, 'BTOW3.SA': {2015: 51.53851005883385, 2016: 44.8766768778324, 2017: 37.82624008178883, 2018: 28.102685346893097, 2019: 40.610198199484834, 2020: 45.63492063492063}, 'WEGE3.SA': {2015: 29.04629568162771, 2016: 20.417983053408694, 2017: 14.691519912317894, 2018: 23.65182624442001, 2019: 12.363907200496495, 2020: 46.66773431693059}, 'ITUB4.SA': {2015: 25.684997781423753, 2016: 19.146231930567005, 2017: 15.206064144768739, 2018: 28.817874021335587, 2019: 18.424106664124775, 2020: 45.213991230064984}, 'BBAS3.SA': {2015: 46.03704780847024, 2016: 30.13645556938046, 2017: 27.294988974337496, 2018: 43.24986947539893, 2019: 20.929829022200064, 2020: 58.286981851334964}, 'B3SA3.SA': {2015: 20.408398517908605, 2016: 25.492304232567232, 2017: 13.647302811687819, 2018: 29.13132745018055, 2019: 14.231530205537815, 2020: 42.687741180836376}, 'MOVI3.SA': {2015: nan, 2016: nan, 2017: 39.285931215455165, 2018: 40.5945655236307, 2019: 20.034250511972054, 2020: 65.71809662426533}, 'AZUL4.SA': {2015: nan, 2016: nan, 2017: 17.14285488927662, 2018: 47.19565512966372, 2019: 24.91710126385561, 2020: 83.41611855988668}, 'IRBR3.SA': {2015: nan, 2016: nan, 2017: 6.0834261004924155, 2018: 9.88859148803348, 2019: 15.05290894618084, 2020: 87.41285870315963}}
Os drawdowns estão calculados mas a visualização não é das melhores. Vamos criar um dataframe onde os ativos estarão nas linhas e cada ano será uma nova coluna:
table = pd.DataFrame(columns=years, index=tickers)
table
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
|---|---|---|---|---|---|---|
| ^BVSP | NaN | NaN | NaN | NaN | NaN | NaN |
| PETR4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| VALE3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| VVAR3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| EQTL3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| LREN3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| GOLL4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| BTOW3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| WEGE3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| ITUB4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| BBAS3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| B3SA3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| MOVI3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| AZUL4.SA | NaN | NaN | NaN | NaN | NaN | NaN |
| IRBR3.SA | NaN | NaN | NaN | NaN | NaN | NaN |
O próximo passo é preencher o dataframe com os valores do dicionário calculado anteriormente:
for ticker in all_drawdowns:
table.loc[ticker] = all_drawdowns[ticker]
table
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
|---|---|---|---|---|---|---|
| ^BVSP | 25.584 | 12.0354 | 12.0054 | 20.3507 | 10.0016 | 46.8158 |
| PETR4.SA | 55.3708 | 38.8646 | 27.6569 | 46.9551 | 17.2438 | 63.3561 |
| VALE3.SA | 56.0826 | 35.5699 | 28.093 | 20.418 | 25.9305 | 40.5509 |
| VVAR3.SA | 82.8794 | 27.1137 | 27.8978 | 50.447 | 36 | 75.3606 |
| EQTL3.SA | 14.3316 | 11.2926 | 11.8055 | 21.7193 | 11.6313 | 40.9665 |
| LREN3.SA | 28.1402 | 21.7093 | 13.1858 | 27.7115 | 10.9165 | 50.6158 |
| GOLL4.SA | 84.2867 | 53.8369 | 35.8222 | 61.0297 | 33.203 | 85.6594 |
| BTOW3.SA | 51.5385 | 44.8767 | 37.8262 | 28.1027 | 40.6102 | 45.6349 |
| WEGE3.SA | 29.0463 | 20.418 | 14.6915 | 23.6518 | 12.3639 | 46.6677 |
| ITUB4.SA | 25.685 | 19.1462 | 15.2061 | 28.8179 | 18.4241 | 45.214 |
| BBAS3.SA | 46.037 | 30.1365 | 27.295 | 43.2499 | 20.9298 | 58.287 |
| B3SA3.SA | 20.4084 | 25.4923 | 13.6473 | 29.1313 | 14.2315 | 42.6877 |
| MOVI3.SA | NaN | NaN | 39.2859 | 40.5946 | 20.0343 | 65.7181 |
| AZUL4.SA | NaN | NaN | 17.1429 | 47.1957 | 24.9171 | 83.4161 |
| IRBR3.SA | NaN | NaN | 6.08343 | 9.88859 | 15.0529 | 87.4129 |
Muito melhor! O último passo é criar uma coluna para a média simples dos drawdowns e ordenar da menor média para a maior:
table["Average"] = table.mean(axis=1)
table = table.sort_values("Average")
table
| 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | Average | |
|---|---|---|---|---|---|---|---|
| EQTL3.SA | 14.3316 | 11.2926 | 11.8055 | 21.7193 | 11.6313 | 40.9665 | 18.624472 |
| ^BVSP | 25.584 | 12.0354 | 12.0054 | 20.3507 | 10.0016 | 46.8158 | 21.132157 |
| B3SA3.SA | 20.4084 | 25.4923 | 13.6473 | 29.1313 | 14.2315 | 42.6877 | 24.266434 |
| WEGE3.SA | 29.0463 | 20.418 | 14.6915 | 23.6518 | 12.3639 | 46.6677 | 24.473211 |
| LREN3.SA | 28.1402 | 21.7093 | 13.1858 | 27.7115 | 10.9165 | 50.6158 | 25.379846 |
| ITUB4.SA | 25.685 | 19.1462 | 15.2061 | 28.8179 | 18.4241 | 45.214 | 25.415544 |
| IRBR3.SA | NaN | NaN | 6.08343 | 9.88859 | 15.0529 | 87.4129 | 29.609446 |
| VALE3.SA | 56.0826 | 35.5699 | 28.093 | 20.418 | 25.9305 | 40.5509 | 34.440821 |
| BBAS3.SA | 46.037 | 30.1365 | 27.295 | 43.2499 | 20.9298 | 58.287 | 37.655862 |
| MOVI3.SA | NaN | NaN | 39.2859 | 40.5946 | 20.0343 | 65.7181 | 41.408211 |
| BTOW3.SA | 51.5385 | 44.8767 | 37.8262 | 28.1027 | 40.6102 | 45.6349 | 41.431539 |
| PETR4.SA | 55.3708 | 38.8646 | 27.6569 | 46.9551 | 17.2438 | 63.3561 | 41.574546 |
| AZUL4.SA | NaN | NaN | 17.1429 | 47.1957 | 24.9171 | 83.4161 | 43.167932 |
| VVAR3.SA | 82.8794 | 27.1137 | 27.8978 | 50.447 | 36 | 75.3606 | 49.949755 |
| GOLL4.SA | 84.2867 | 53.8369 | 35.8222 | 61.0297 | 33.203 | 85.6594 | 58.972989 |
Considerações finais
- O drawdown é uma forma de expor a volatilidade de um ativo. Note que mesmo em um ano relativamente calmo e direcional para a bolsa como 2019, ativos como GOLL4 e BTOW3 chacoalharam bastante. Em contrapartida, EQTL3 costuma ser bastante estável e mesmo em um ano de queda brutal como 2020, ela teve o menor drawdown da lista;
- IRBR3, AZUL4 e MOVI3 fizeram seu IPO em 2017 e portanto não possuem drawdown antes disso;
- A média é apenas uma pista, mas não conta a história toda. Note como IRBR3 possuía uma média extremamente baixa até o ano de 2020, onde apresentou o maior tombo de todos (inclusive maior que as aéreas!)
Agora que já sabemos calcular o drawdown podemos utilizar essa medida nas nossas estratégias de trade. Fique ligado para os próximos posts, onde compareremos estratégias não somente no seu retorno financeiro, mas no seu drawdown máximo.
