Entenda o que é Valor Esperado (EV) e Sua Utilidade Para um Trader

No seu famoso livro Iludidos Pelo Acaso (Fooled by Randomness no original), o autor Nassim Taleb descreve uma situação onde um colega de trabalho questiona se ele acha que o mercado vai subir ou descer. "Acho que sobe", diz Taleb. No dia seguinte, o amigo retorna furioso ao perceber que Taleb havia embolsado uma boa grana efetuando um trade na direção contrária, isto é, que o mercado ia cair. Questionado por ter dito uma coisa e feito outra, o trader responde que havia uma chance maior de ser um dia de alta, porém, caso fosse um dia de baixa, o mercado cairia com força.

Se você, como o colega do autor, ainda vê uma contradição na ação do trader, não se preocupe. Nesse artigo, exploraremos o conceito de Valor Esperado (também conhecido como Esperança ou Expectativa Matemática), e aprenderemos como utilizar esse importante conceito de forma prática no dia-a-dia de um trader.

Definindo o Valor Esperado

Imagine a seguinte situação: um amigo propõe uma aposta, onde vocês rolarão os dados. Se o número for par, você ganha R$10. Se for ímpar, você precisa pagá-lo R$11. Você aceitaria essa aposta?

Mesmo que você ainda não saiba o que é Valor Esperado (EV), a resposta provavelmente é não. Não parece justo que ele ganhe mais do que você, considerando que a chance de vitória é a mesma para ambos.

Intuitivamente fica simples perceber que essa aposta é ruim para você. Matemáticamente, como podemos ter certeza? Daí o conceito de Valor Esperado.

Definimos o Valor Esperado como a soma das probabilidades de um determinado evento acontecer ponderadas por quanto você ganha (ou perde) em cada situação. Em outras palavras:

\[ EV = P_{gain} \times payoff + P_{loss} \times risk \]

Onde \(P_{gain}\) é a probabilidade de acerto, \(P_{loss}\) é a probabilidade de erro, \(payoff\) é quanto você ganha se acertar e \(risk\) é quanto você perde se errar.

Podemos então calcular o valor esperado da aposta substituindo os valores na fórmula:

\[ EV = 0.5 \times 10 + 0.5 \times -11 = -0.5 \]

O valor esperado negativo nos indica que a aposta, no longo prazo, é perdedora, e que é "esperado" que percamos R$0.50 cada vez que jogamos os dados. Isso é extremamente, pois significa que mesmo que haja uma sequência de eventos onde ganhemos 3x seguidas (o que tem uma probabilidade não-desprezível de 12,5%), ainda assim estamos fazendo um mau negócio.

Valor Esperado na prática

Agora que o conceito de EV já foi definido, vamos explorá-lo em algumas situações típicas.

Apostas esportivas

Talvez o exemplo mais flagrante da utilidade do Valor Esperado se dá nas apostas esportivas. Apostas esportivas normalmente são eventos binários, ou seja, ou uma situação acontece, ou outra mutuamente excludente. Por exemplo:

• Ou o Vasco ganha, ou o Vasco não ganha (empata ou perde).
• Ou o Charles do Bronx finaliza por guilhotina no 3º round, ou ele não finaliza por guilhotina no 3º round.

Ou o Trump é eleito, ou ele não é eleito.

• Embora tecnicamente uma eleição não seja um evento esportivo, seu resultado é binário, então vamos usar a licença-poética aqui para entender "esportivas" como "recreativas".

Como o evento é binário, se definirmos \(P_{gain} = p\), naturalmente segue que \(P_{loss} = 1 - p\), uma vez que a soma dos dois eventos precisa ser 1.

O que resta agora é definir quanto que recebemos em retorno por uma aposta, ou seja, o valor que estamos arriscando (\(risk\)). Essa proporção é o que chamamos de odds. Uma odd de 2:1 significa que, para cada real apostado, recebemos 2 de volta caso ganhemos. Usando os termos que vimos anteriormente, \(risk = 1\) e \(payoff = 2\).

Nesse exemplo, substituindo na nossa fórmula do EV, segue que:

\[ EV = p \times 2 + (1 - p) \times (-1) = 3p - 1 \]

Onde \(p\) é a probabilidade de acerto.

Tá, mas até agora isso não quer dizer muito. Como podemos interpretar essa equação?

Descobrindo seu edge

Se um EV negativo significa que você irá perder dinheiro no longo prazo e um EV positivo significa que você irá ganhar dinheiro no longo prazo, naturalmente um \(EV = 0\) representa o seu break-even, ou seja, o limite onde sua aposta passa a ser vencedora ou perdedora.

Aplicando essa condição na equação anterior, temos:

\[EV = 3p - 1 = 0\]

De onde segue que \(p = \dfrac{1}{3}\), ou 33.3%.

Isso significa que, para as odds apresentadas (2:1), o break-even da aposta é 33.3%. Se a chance de sucesso for maior que isso, sua aposta tem uma expectativa matemática positiva. Se for menor, negativa. À diferença entre a probabilidade de sucesso e o break-even damos o nome de edge.

Sendo assim, se o seu julgamento para um determinado evento é uma chance de 50% de acerto e as odds estão 2:1, você tem um edge sobre a casa e portanto a aposta é matematicamente aceitável. Substituindo na fórmula do EV para essas odds:

\[ EV = 3p - 1 = 3 \times 0.5 - 1 = 0.5 \]

Em outras palavras, no longo prazo, para cada real investido você é esperado de obter R$0,50 de retorno.

Exemplo: Final da Libertadores

Certo, já aprendemos o que é Valor Esperado e como podemos utilizar as odds para determinarmos se temos um edge, ou seja, uma vantagem competitiva em relação à nossa contraparte. Vou ilustrar agora como um apostador (ou trader) pode utilizar esse conceito na prática.

A final da Libertadores de 2021 foi entre Palmeiras e Flamengo, este último sendo considerado o favorito, algo que eu também acreditava. A questão então era: quão favorito? Existe um edge nas odds oferecidas?

Fui então ao site do Sportsbet e descobri que eles estavam oferecendo odds de 10:1 no título do Flamengo, limitado a R$10. Essas odds obviamente são fora da realidade, já que se substituirmos na nossa fórmula do EV, descobriremos que o break-even da casa ficaria em \(\dfrac{1}{11}\), ou 9%, algo incompatível com o favoritismo do rubro-negro.

Isso não passou de uma inteligentíssima ação de marketing da empresa, que provavelmente aumentou significativamente sua base de usuários a um risco controlado. Essas odds já seriam suficientes para que eu, que considerava o Flamengo favorito, fizesse a aposta. Porém, pensei: e se eu usar essa aposta, que tem capital limitado, como hedge (proteção, não confundir com edge) de uma aposta maior? Em outras palavras: consigo abater essas odds irreais de uma aposta contrária no Palmeiras de modo a embolsar um prêmio maior?

A mesma casa pagava odds de 2.63:1 no título do Palmeiras, o que correspondia a 27,5% de probabilidade. Por si só, isso já me parecia uma odd bastante atrativa: certamente o Flamengo era favorito, mas não nessa proporção!

O Resultado

No final, essas foram as apostas que eu fiz:

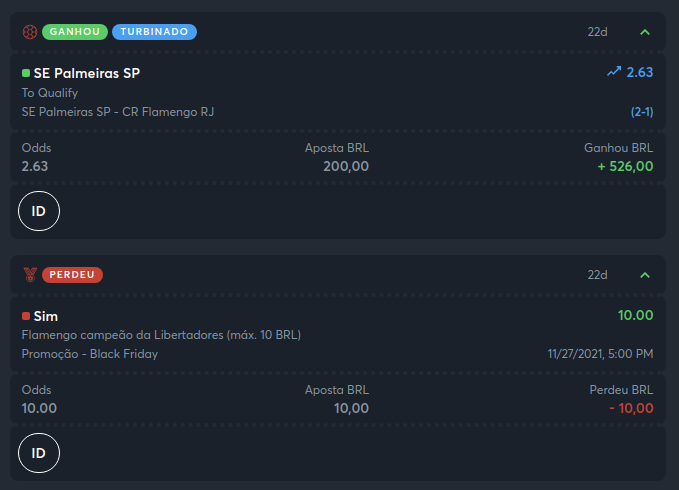
Vamos entender a aposta e calcular as odds reais que a casa de apostas estava oferecendo:

• R$10 no título do Flamengo, que caso se concretizasse me retornaria R$100;
• R$200 no título do Palmeiras, que caso se concretizasse me retornaria R$526.

Assim, haviam duas possibilidades:

Possibilidade 1: Flamengo campeão, eu ganho R$100 da aposta vencedora mas perco R$200 da aposta feita no Palmeiras. Resultado: aposto R$210 e fico com R$100, um prejuízo de -R$110.

Possibilidade 2: Palmeiras campeão, eu perco R$10 da aposta no Flamengo mas embolso R$526 da aposta no Palmeiras. Resultado: aposto R$210 e fico com R$526, um lucro líquido de R$316.

Resumidamente, eu estava arriscando R$110 (Flamengo campeão) para ganhar R$526 (Palmeiras campeão), odds de quase 5:1!

Vamos descobrir o break-even da aposta:

\[ EV = p \times 526 + (1 - p) \times (-110) \]
\[ EV = 636p - 110 = 0 \]
\[ p = \dfrac{110}{636} \approx 0.173 \]

Ou seja: a casa estava "precificando" o título do Palmeiras em 17,3%. Se o meu julgamento inicial era um favoritismo de 60-40 para o Flamengo, eu fui praticamente obrigado a fazer a aposta no underdog.

Valor Esperado no Poker

Outra aplicabilidade bastante comum do EV é como critério de aposta no jogo de Poker. Nesse jogo de cartas, os jogadores fazem apostas a cada turno, e o total apostado é acrescentado ao pot. O vencedor da mão leva todo o valor do pot.

Assim, à medida que os turnos avançam, o pot cresce e portanto o prêmio fica maior. Dessa forma, ao ser confrontado com a decisão de pagar ou não uma determinada aposta, o jogador precisa calcular qual o EV da jogada, isso é, se pagar a aposta é matematicamente positivo no longo prazo (\(EV > 0 \)).

Suponha que o pot contenha R$1000 no flop e um adversário vai all-in apostando R$800. Você julga possuir 6 outs, isto é, 6 cartas que melhoram a sua mão e tornam-a vencedora. Sem entrar em muitos detalhes do jogo, isso equivale aproximadamente a uma chance de 24% de que alguma dessas 6 cartas irá aparecer até o fim. Deve você pagar a aposta?

Bem, nesse caso \(risk = 800\) e \(payoff = 1000 + 800 + 800 = 2600\) (R$1000 já estavam no pot, R$800 apostados pelo adversário e R$800 apostados por você). Assumindo uma chance de vitória de 24%, seu EV então é:

\[ EV = 0.24 \times 2600 + (1 - 0.24) \times (-800) \]
\[ EV = 624 - 608 = 16 > 0 \]

Sendo o EV positivo, o jogador está "matematicamente autorizado" a pagar a aposta.

Problemas do Valor Esperado

Sempre que calculamos o Valor Esperado devemos nos atentar a alguns problemas típicos. Alguns deles:

• Pressupomos um longo prazo. Assim, nada adianta justificar uma decisão pelo EV se é uma situação atípica ou marginalmente vencedora;
• Nosso julgamento das probabilidades pode ser enviesado. Por exemplo, o fato de ter achado a probabilidade de 17,3% do Palmeiras ser campeão um escândalo pode ter sido enviesado pelo fato de eu ser vascaíno e estar fervorosamente torcendo contra;
• Não há Valor Esperado se há chance de ruína. Um exemplo clássico é a roleta russa: mesmo que você ganhe R$1 bilhão para apertar o gatilho com uma probabilidade de \(\dfrac{5}{6}\)​ de sucesso, o \( risk \) (colocar uma bala na cabeça) inviabiliza a operação.

No mundo do trading é bastante comum cometermos o primeiro erro, influenciados principalmente por situações atípicas ou um espaço amostral pequeno. Portanto, um backtest realizado com poucas operações é extremamente sensível a ruídos, o que na prática significa que aquela probabilidade não representa a realidade.

Já a chance de ruína é muito comum nos jogos de poker: por mais que uma jogada tenha o EV positivo, às vezes é melhor esperar uma melhor oportunidade, mais segura, do que correr o risco de ser prematuramente eliminado.

No mundo dos investimentos, essa é a razão pela qual nunca devemos ir all-in em uma única operação. Por mais certos que estejamos e por mais positivo que seja o nosso EV, o risco de ser tirado do jogo não compensa o resultado.

Valor Esperado para Traders

Agora que já aprendemos a calcular e aplicar o EV e entendemos suas limitações, podemos nos aprofundar no seu uso para traders.

Na plataforma do QuantBrasil temos um Simulador de Estratégias onde qualquer um pode realizar o backtest de sua estratégia favorita.

O resultado a seguir é o resultado da estratégia do 123 de Compra para JBSS3 nos 120 minutos quando esse ativo está no Éden dos Traders:

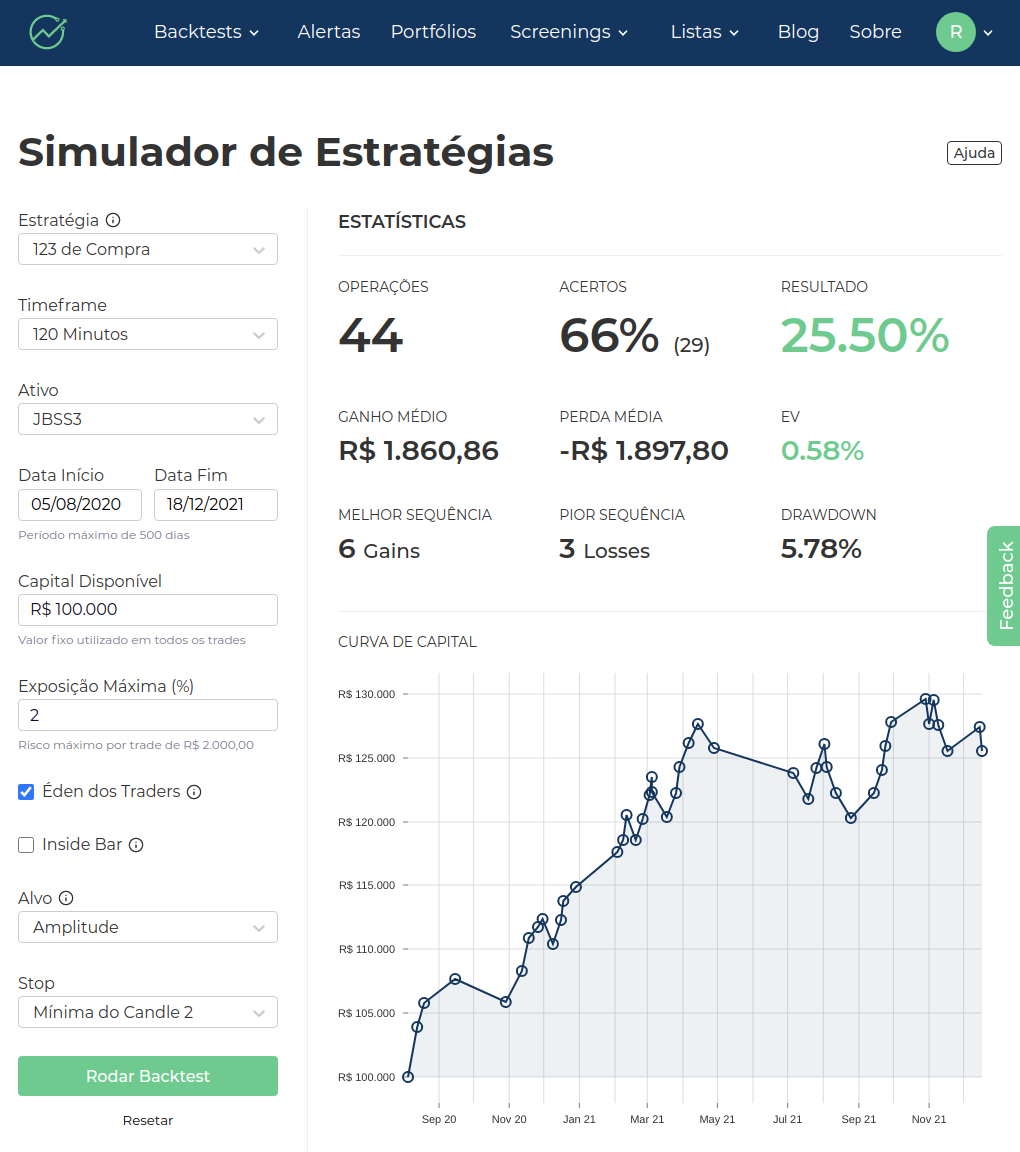
Quer rodar os seus próprios backtests? Crie sua conta no QuantBrasil. Não leva nem 1 minuto!

O resultado é bastante positivo e o EV (Valor Esperado) é de 0.58%. Como chegamos a esse número?

Bem, veja que acertamos 29/44 de operações, o que corresponde a 66% de assertividade. Como limitamos o nosso risco a 2% do capital inicial de R$100,000, nosso \( risk \) vai girar em torno de R$2,000 (na prática o valor sempre será diferente, pois há gaps, o lote precisa ser múltiplo de 100 ações, etc).

A perda média acabou ficando em R$1897,80 (próximo ao nosso risco máximo teórico estabelecido) e o ganho médio foi de R$1860,86. No final, é como se o "mercado" estivesse nos oferecendo odds bem próximas de 1:1 para aplicar essa estratégia.

Substituindo todos esses valores na fórmula do EV, segue que:

\[ EV = 0.66 \times 1860,86 + 0.34 \times (-1897,80) \]
\[ EV = 1228,17 - 645,25 = 582,92 \]

Isso significa que, para um capital de R$100,000 a um risco máximo de 2%, o valor esperado por trade é de R$582, ou 0.58% do capital.

O EV não é a única coisa que importa

Observadas todas as ressalvas feitas ao Valor Esperado, é inegável que esse seja uma das métricas mais importantes na tomada de decisão de um trader. Ainda assim, o EV por si só não carrega todas as informações.

Considere o seguinte backtest, também realizado para JBSS3 nos 120 minutos, mas dessa vez sem o filtro de Éden dos Traders e com um risco fixo de 2:1.

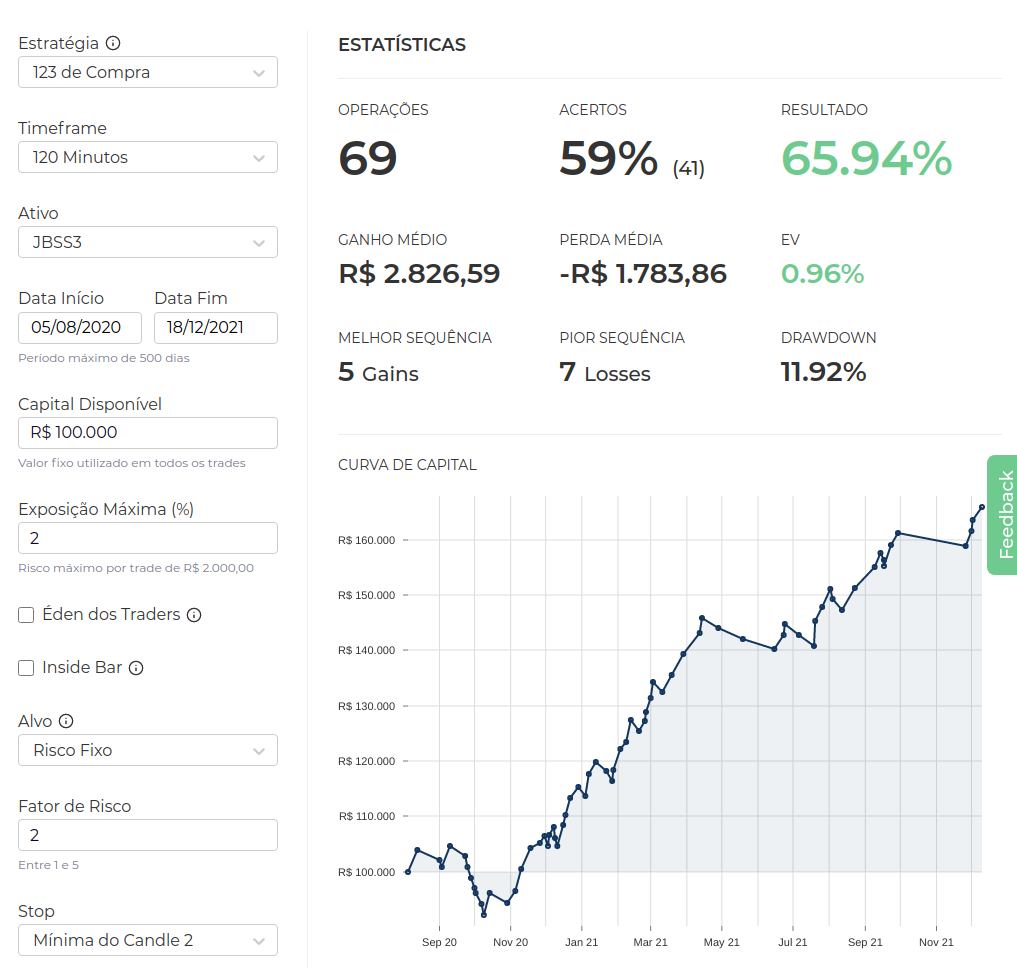
Aqui, temos um EV impressionante de 0.96%, o que significa que um trader executando essa estratégia durante esse período tinha uma expectativa matemática de aumentar o seu patrimônio em praticamente 1% a cada trade.

Tão bom quanto pareça, essa performance impressionante não vem de graça. Primeiro, a taxa de erro aumentou de 34% para 41%. Segundo e principal, o drawdown mais que dobrou, atingindo quase 12% (a maior sequência de perdas indo de 3 para 7).

Em outras palavras, nosso retorno aumentou, mas também o nosso risco. A combinação que melhor funciona sempre será uma função do seu apetite ao risco e força mental durante os trades. Pergunte a si mesmo: continuaria mantendo a mesma estratégia depois dela falhar 7x em sequência?

Atenção: a dinâmica do mercado muda

Você fez o dever de casa: estudou a estratégia, realizou o backtest, aferiu o EV, e agora? Deve colocar todo seu dinheiro na estratégia em questão?

Antes de sair fazendo isso, lembre-se que o mercado é dinâmico e backtests sempre representam o passado. Em outras palavras, não é porque uma estratégia teve \(EV = 0.98 \) nos últimos 2 anos que ela continuará tendo pelos próximos 2. Por exemplo, JBSS3 foi um dos papeis mais fortes do Ibovespa em 2021, então naturalmente a maior parte das estratégias nesse ativo foi lucrativa.

Se o EV não é garantia de nada, por que me preocupar em calculá-lo então?

Essa pergunta é bastante pertinente e não nos cabe explicar com rigor matemático nesse momento. No entanto, é importante entender que um papel que teve a dinâmica que JBSS3 apresentou naquele período, observados os mesmos parâmetros da estratégia, teve um EV tão alto quanto 0,98%. É possível presumir, então, que se formos capazes de identificar papeis apresentando uma dinâmica parecida, o resultado pode ser parecido.

No QuantBrasil, a cada semana atualizamos o ranking com os ativos que melhor performaram em uma determinada estratégia nos últimos 500 dias (crie sua conta para visualizar o ranking de backtests). Essa é uma forma de estar sempre acompanhando os ativos cuja estratégia está funcionando.

Além disso, nosso screening de momentum gera sempre uma lista atualizada dos ativos que estão performando melhor nos últimos meses. Sendo a estratégia de 123 de compra majoritariamente seguidora de tendência, é razoável assumir que ativos com maior momentum apresentem um resultado melhor no backtest dessa estratégia (no momento de escrita desse artigo JBSS3 é o 3º na lista de momentum).

Conclusão

O Valor Esperado (ou Esperança/Expectativa Matemática) é uma métrica extremamente relevante para tomadas de decisão. Vimos que sua aplicabilidade é diversa no cotidiano, indo desde apostas esportivas, passando pelo poker e sendo crucial para traders.

No QuantBrasil é possível rodar backtests de diversas estratégias e saber exatamente o EV, ou quanto você é esperado de ganhar por trade, considerando a dinâmica do mercado no período de teste.

Ainda assim, o EV precisa ser observado com atenção: ele é irrelevante caso haja risco de ruína e estará sempre sujeito a alteração nas probabilidades. Ferramentas como o ranking de backtests e o screening de momentum são úteis para minimizar a chance de calcular um EV que já não representa a realidade.

Por fim e mais importante, o EV nos ajuda a entender qual é o payoff de uma estratégia e porquê podemos achar que um determinado evento é mais provável e ainda assim fazer uma aposta na direção contrária. Como diria Nassim Taleb no seu livro Skin in the Game:

What matters in life isn't how frequently one is "right" about outcomes, but how much one makes when one is right.